Ruffini es un método que nos permite dividir un polinomio entre un binomio , monomio o variable numérica, permitiéndonos localizar las raíces de un polinomio para factorizar en binomios, este método nos posibilita realizar la división o descomposición de un polinomio algebraico n, en un binomio algebraico.
Mediante este método se puede resolver ecuaciones de segundo grado, así como, ecuaciones de grado mayor.
Para resolver ecuaciones de segundo grado por Ruffine se sigue los siguientes pasos:
1 – Identificamos los coeficientes de cada término, que son los números que van delante de la incógnita. Para la ecuación anterior, los represento en verde para identificarlos:
2 – Trazamos dos líneas perpendiculares de esta forma:
3 – Colocamos los coeficientes ordenados por su grado de mayor o menor:
En la regla de Ruffini, el grado va disminuyendo de 1 en 1 y cada grado tiene su lugar. Por ejemplo si no tuviérmos ningún término que tenga x², en el lugar del grado 2, se colocaría un 0.
Los números que hemos escrito hasta ahora en el método de Ruffini, es equivalente a escribir la ecuación, es decir:
4 – Ahora escribimos un número a la izquierda de la línea vertical. Más adelante explicaremos qué número colocar aquí y por qué. De momento, empezamos con el 1.
Ese número corresponde al número (a) del binomio x – a:
En este caso, escribir ahí un 1, significa el binomio (x – 1) en el método de Ruffini
5 – Empezamos a ejecutar el método. El primer hueco de la segunda fila, siempre se deja libre:
6 – Se hace la suma de la primera columna y el resultado de pone abajo:
7 – Se multiplica el número de la izquierda por el resultado de la suma de la primera columna. El resultado se coloca en el hueco de la segunda columna:
8 – Se realiza la suma de la segunda columna:
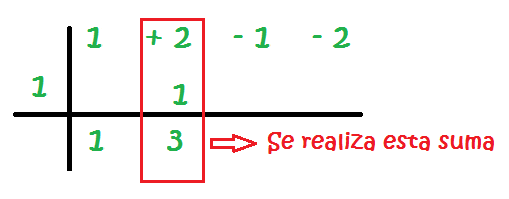
9 – Se multiplica el número de la izquierda por el resultado de la suma de la segunda columna. El resultado se coloca en el hueco de la tercera columna:
10 – Así sucesivamente hasta completar todas las columnas:
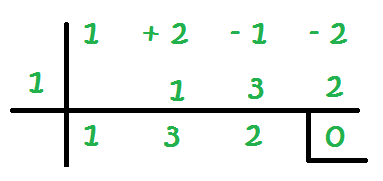
El objetivo es que en la última columna tengamos un 0. Esta es la explicación de qué número colocar a la izquierda de la línea:
Si no tenemos un cero, tendríamos que probar con otro número a la izquierda de la línea vertical y reiniciar el proceso.
Repetimos los pasos ya mencionados hasta quedar de la siguiente manera
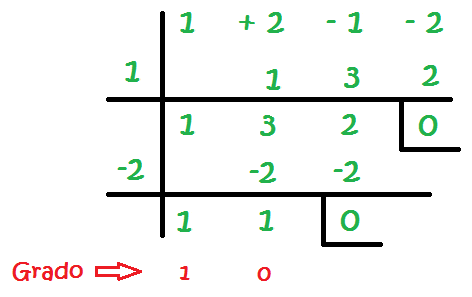
1 – Identificamos los coeficientes de cada término, que son los números que van delante de la incógnita. Para la ecuación anterior, los represento en verde para identificarlos:
2 – Trazamos dos líneas perpendiculares de esta forma:
3 – Colocamos los coeficientes ordenados por su grado de mayor o menor:
En la regla de Ruffini, el grado va disminuyendo de 1 en 1 y cada grado tiene su lugar. Por ejemplo si no tuviérmos ningún término que tenga x², en el lugar del grado 2, se colocaría un 0.
Los números que hemos escrito hasta ahora en el método de Ruffini, es equivalente a escribir la ecuación, es decir:
4 – Ahora escribimos un número a la izquierda de la línea vertical. Más adelante explicaremos qué número colocar aquí y por qué. De momento, empezamos con el 1.
Ese número corresponde al número (a) del binomio x – a:
En este caso, escribir ahí un 1, significa el binomio (x – 1) en el método de Ruffini5 – Empezamos a ejecutar el método. El primer hueco de la segunda fila, siempre se deja libre:
6 – Se hace la suma de la primera columna y el resultado de pone abajo:
7 – Se multiplica el número de la izquierda por el resultado de la suma de la primera columna. El resultado se coloca en el hueco de la segunda columna:
8 – Se realiza la suma de la segunda columna:
9 – Se multiplica el número de la izquierda por el resultado de la suma de la segunda columna. El resultado se coloca en el hueco de la tercera columna:
10 – Así sucesivamente hasta completar todas las columnas:
El objetivo es que en la última columna tengamos un 0. Esta es la explicación de qué número colocar a la izquierda de la línea:
Si no tenemos un cero, tendríamos que probar con otro número a la izquierda de la línea vertical y reiniciar el proceso.
Repetimos los pasos ya mencionados hasta quedar de la siguiente manera
Nos quedan tres ecuaciones de primer grado para despejar, de donde obtenemos las tres soluciones
Tomado de ekuatio: https://ekuatio.com/la-regla-de-ruffini/
OBSERVA LO SIGUIENTE:
El discriminante es la expresión del radical de la formula cuadrática (b2-4ac).
El signo del discriminante puede ser utilizado para encontrar el numero de soluciones de las ecuaciones cuadráticas correspondientes, de la forma ax2+bx+c = 0.
Si el discriminante b2-4ac da como resultado un número negativo, la ecuación no tiene soluciones reales.
Si el discriminante b2-4ac nos da como resultado 0, la ecuación tiene una única solución.
Si el discriminante b2-4ac da como resultado un número positivo, entonces la ecuación consta de dos respuestas ±.
Al discriminante se lo simboliza con ∆
Para la resolución de la ecuación cuadrática se debe seguir lo siguiente:
Resuelva la ecuación cuadrática
El signo del discriminante puede ser utilizado para encontrar el numero de soluciones de las ecuaciones cuadráticas correspondientes, de la forma ax2+bx+c = 0.
Si el discriminante b2-4ac da como resultado un número negativo, la ecuación no tiene soluciones reales.
Si el discriminante b2-4ac nos da como resultado 0, la ecuación tiene una única solución.
Si el discriminante b2-4ac da como resultado un número positivo, entonces la ecuación consta de dos respuestas ±.
Al discriminante se lo simboliza con ∆
Para la resolución de la ecuación cuadrática se debe seguir lo siguiente:
Resuelva la ecuación cuadrática
nuestro discriminante es b2-4ac, reemplezando tenemos ∆=12-4(3)(-5)Simplifique:
en este punto ya sabemos que nuestro discriminante es positivo pues la raíz de 61 es 7.81...Esto significa que tenemos dos raíces:
OBSERVA EL SIGUIENTE VÍDEO:
Este método es la técnica que se utiliza cuando tenemos una ecuación de segundo grado o cuadrática o del tipo ax2+bx+c = 0, en donde a debe ser distinta de cero, y la transformamos primero en un trinomio cuadrado perfecto con el fin de completar la ecuación para crear un cuadrado de un binomio y de esta manera poder despejar la incógnita que es x.
Forma de resolución de ecuaciones causticaras completando el trinomio cuadrado perfecto
Para la resolución de ecuaciones cuadrática completando el trinomio se debe seguir los siguientes pasos:
De esta manera es como formamos nuestro trinomio cuadrado perfecto; cuyo primer término es el cuadrado de x su segundo termino es el doble del producto de x por b/2 y su tercer termino es el cuadrado de la mitad de b.
En este punto la ecuación cuadrática ya puede ser resuelta mediante cualquiera de los casos de resolución ya estudiados previamente.
OBSERVA EL VÍDEO PARA MAYOR ENTENDIMIENTO:
Una ecuación de segundo grado se la dice incompleta cuando alguno de sus coeficientes b o c, o amabas, son iguales a cero por tanto podemos encontrarnos con tres tipos de ecuaciones cuadráticas incompletas.
Son de la forma: ax2+bx = 0; c=0 ax2+c
= 0; b=0 ax2 = 0; b=0, c=0
Formas de resolución de ecuaciones cuadráticas incompletas
1. ax2 = 0
La solución es x = 0.
2. ax2 + bx = 0
Extraemos factor común x:
Como tenemos un producto igualado a cero o un factor
es cero o el otro factor es cero o los dos son cero.
es cero o el otro factor es cero o los dos son cero.
3. ax2 + c = 0
1. En primer lugar pasamos el término c al segundo miembro cambiado de signo.
2. Pasamos el coeficiente a al 2º miembro, dividiendo.
3. Se efecúa la raí cuadrada en los dos miembros.
Se puede resolver cualquier ecuación cuadrática completa con la formula general o formula cuadrática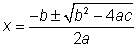 
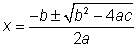, es muy útil para resolver ecuaciones cuadráticas que son difíciles o imposibles de factorar y usarlas puede ser mucho mas rápido que completar el cuadrad, ésta formula puede ser utilizada para resolver cualquier ecuación cuadrática que este de la forma ax2+bx+c
= 0.
, es muy útil para resolver ecuaciones cuadráticas que son difíciles o imposibles de factorar y usarlas puede ser mucho mas rápido que completar el cuadrad, ésta formula puede ser utilizada para resolver cualquier ecuación cuadrática que este de la forma ax2+bx+c
= 0.
Para su resolución se debe seguir los siguientes pasos:
- Transformar la ecuación a la forma ax2+bx+c = 0.
- Identifica los coeficientes, a, b, y c. Ten cuidado de incluir su correspondiente signo.
- Sustituye los valores de los coeficientes en la formula cuadrática.
- Simplifica lo mas posible.
- Utiliza ± en frente del radical para separar la solución en dos valores.
- Simplificar ambos valores para obtener las posibles soluciones de la ecuación.
Formas de resolución de ecuaciones cuadráticas por fórmula general
 | |||||
 |
Restar 6x de cada lado y sumar 16 a ambos lados para transformar la ecuación a su forma
 . | ||||
 |
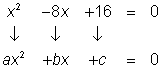Identificar los coeficientes a, b, y c. x2= 1x2, entonces a = 1. Como 8x está siendo restado, b es negativo.
a = 1, b = -8, c = 16.
| ||||
 |
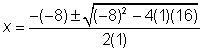Aplicar la fórmula cuadrática
| ||||
 |
Simplificar
| ||||
 |
Como la raíz cuadrada de 0 es 0, y sumar o restar 0 dan el mismo resultado, existe sólo un valor posible
| ||||
Respuesta
|
x = 4
| ||||
Tomado de http://www.montereyinstitute.org/courses/Algebra1/COURSE_TEXT_RESOURCE/U10_L1_T3_text_final_es.html\
REVISA LA SIGUIENTE PRESENTACIÓN:
REVISA LA SIGUIENTE PRESENTACIÓN:
Para la resolución de ecuaciones cuadráticas por factorización o también llamada por descomposición factorial; es importante, que se encuentre de la forma ax2+bx+c y que ésta sea factorable, caso contrario no podrá ser resuelto por éste método, para su resolución se debe seguir los siguientes pasos:
- Se debe realizar la simplificación de la ecuación dada y dejarla de la forma ax2+bx+c = 0
- Realizar la correspondiente factorización del trinomio de la forma ax2+bx+c, y obtener su resultado ( producto de binomios).
- Los factores obtenidos, deberán ser igualados a cero, de esta manera se obtendrán dos ecuaciones simples, las cuales deberán ser resueltas.
Para mayor entendimiento OBSERVA LA PRESENTACIÓN SIGUIENTE
Las ecuaciones cuadráticas se dividen en los siguientes tipos que son:
- Ecuación cuadrática pura: Es aquella que se encuentra integrada únicamente por una incógnita de grado dos, acompañada por una o "n" constantes, ax2+b = 0.
- Ecuación cuadrática mixta: Este tipo de ecuación solo contiene una incógnita de segundo grado y una de grado uno igualada a cero, ax2+xb = 0.
- Ecuación cuadrática completa: Es aquella que esta compuesta por una variables de grado 2, una de grado 1 y una constante igualada a cero, ax2+xb+c = 0
Suscribirse a:
Entradas (Atom)
